The A-Team

"The A-Team» erschien im Jahr 2010. Der Film basiert auf der gleichnamigen Fernsehserie «The A-Team» aus den 80er Jahren.
Die Geschichte handelt von den vier Mitgliedern des A-Team, Kriegsveteranen des Irakkriegs. Das Team wird für ein Verbrechen verurteilt, das es nicht begangen hat und wird verhaftet. Nach einer spektakulären Flucht machen sie sich auf die Suche nach dem eigentlichen Verbrecher.

You can't fly a tank

Die ausgewählte Szene zur Analyse und Berechnung ist die "You can't fly a tank" Szene.

Die Szene beginnt damit, dass das Team in einem Flugzeug abgeschossen wird. Als nächstes ist zu sehen, wie die vier Veteranen in einem Panzer, der sich im Flugzeug befand, am Abstürzen sind. Es öffnen sich drei Rundkappenfallschirme, die den Fall des Panzers verlangsamen. Zwei von den drei Fallschirmen werden abgeschossen, so dass jetzt nur noch ein Fallschirm den Sturz ein wenig verlangsamt. Das Team will den Panzer nun mit dem Rückstoss der Kanone steuern, so dass sie in einem See eine halbe Meile (0.804672 km) entfernt landen könnten. Dies gelingt ihnen und es ist zu sehen, wie der Panzer über dem See ist.

Berechnungen

Variablen

• Gewichtskraft g = 9.81 N/kg
• Masse des Panzers m = 17'463.31 kg
• Schussgeschwindigkeit der Panzerkanone: 12 Schüsse pro Minute
• Masse eines Projektils m = 13.1 kg
• Geschwindigkeit eines Projektils v = 1021.08 m/s
• Höhe des Sturzes aus dem Flugzeug h = 10'000 m
• Fläche Rundkappenfallschirm A = 115 m^2
• Widerstandsbeiwert cW = 1.4
• Zurückzulegende Strecke s = 804 m
• Zeitdauer fallender Panzer mit drei Fallschirmen t = 93 s

Darstellung des Bewegungsablaufs der Szene

Luftdichte

Wie bereits bei der ersten Szene erwähnt, ist die Luftdichte keine konstante Grösse. Luftdichte und Luftdruck nehmen je höher man steigt exponentiell ab. Dadurch stellt sich heraus, dass auch der Luftwiderstand nicht als konstant angenommen werden kann.
Der Panzer fällt folglich nicht mit einer konstanten Geschwindigkeit, da die Luftdichte und der Luftwiderstand zunehmen. Um nun zu wissen, wie viele Höhenmeter der Panzer gefallen ist, bis die zwei Fallschirme zerstört werden, muss wieder schrittweise gearbeitet werden, da sich die Luftdichte dazwischen verändert.
Die Daten der Luftdichte werden einer Tabelle der Public Domain Aeronautical Software entnommen. Dazu muss gesagt werden, dass auf die Luftdichte noch andere Faktoren wie die exakte Temperatur und die Luftfeuchtigkeit einen Einfluss haben können. Diese können allerdings nicht bestimmt werden, da sie vom Wetter, der Tageszeit und vom Ort abhängen. Deswegen werden die Daten einer Standard-Atmosphären-Tabelle entnommen.
Die Veränderung der Luftdichte wird vereinfacht alle 500 Meter angepasst. Das heisst, es wird mithilfe einer Exceltabelle ausgerechnet, mit welcher Geschwindigkeit der Panzer fällt und in welcher Zeit er die 500 Meter zurücklegt. Die Berechnungen werden wie bei der ersten Szene mit der Methode der kleinen Schritte gemacht. So wird berechnet, welche Höhe der Panzer nach den 93 Sekunden erreicht, denn nach 93 Sekunden Fallzeit werden die Fallschirme zerstört.

Ausschnitt aus der Tabelle für die Luftdichte

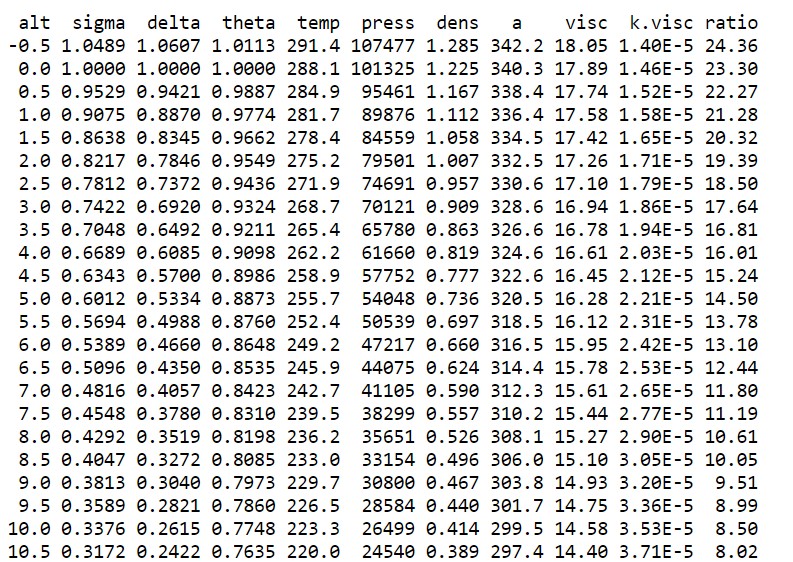
Die erste Spalte, die mit "alt" beschriftet ist, zeigt die Höhe in Kilometer.
Die Spalte mit "dens" zeigt die Luftdichte bei der jeweiligen Höhe in Kilogramm pro Kubikmeter.

Die Tabelle stammt von der Seite Public Domain Aeronautical Software (PDAS):
https://www.pdas.com/atmosTable2SI.html

Höhe der Zerstörung zweier Fallschirme

Mithilfe von Excel konnte schrittweise die gefallene Höhe des Panzers in 93 Sekunden berechnet werden. Die Zerstörung zweier Fallschirme geschieht nach 3'424.9 gefallenen Metern. Das bedeutet, dass der Panzer nun noch 6'575.1 Meter mit nur noch einem Fallschirm fällt.

Drehen der Panzerkanone

Zeit bis zum Aufprall

Nun muss ausgerechnet werden, wie viel Zeit das Team im Panzer hat, um den Panzer 804 Meter in der Horizontalen zu bewegen. Dabei wird gleich vorgegangen, wie bei den Berechnungen oben mit drei Fallschirmen. Das Einzige, was verändert wird, ist die Fläche. Diese beträgt nun noch einen Drittel der Fläche beim Fall mit drei Fallschirmen, da zwei zerstört sind.
Der gesamte Fall des Panzers dauert 226 Sekunden. Abzüglich die 93 Sekunden des Falles mit drei Fallschirmen, hätte das Team 133 Sekunden Zeit, den Panzer zu steuern. Doch das Team beginnt nicht direkt die Schüsse abzufeuern, nachdem die Fallschirme zerstört wurden. Der erste Schuss wird 29 Sekunden nach der Zerstörung der Fallschirme abgegeben. Das heisst, der Panzer fällt zu diesem Zeitpunkt für 122 Sekunden. Aus der erstellten Exceltabelle kann nun abgelesen werden, dass sich der Panzer nach 122 Sekunden Fallzeit in einer Höhe von 5008.9 Meter befindet.

10' 000 m - 5008.89393 m = 4991.10607 m

Folglich fällt das Team noch 4991.1 Meter. Nun kann erneut mithilfe der Exceltabelle ausgerechnet werden, wie viel Zeit noch bleibt, um den Panzer die 804 Meter zu bewegen. Die gesamte Fallzeit des Panzers beträgt 226 Sekunden. Der erste Schuss wird nach 122 Sekunden abgegeben.

226 s - 122 s = 104 s

Das Team hat somit 104 Sekunden Zeit, mit Schüssen den Panzer zu bewegen.

Abgegebene Schüsse

Die Hauptkanone XM35 des Panzers kann 12 Schüsse pro Minute abgeben, das entspricht einem Schuss alle fünf Sekunden.

(104 s)/(5 s)=20.8

In 104 Sekunden kann die Kanone also 20 Schüsse abgeben.

Impulserhaltung

Um herauszufinden, wie stark der Rückstoss der abgeschossenen Munition den Panzer bewegen kann, wird der Satz der Impulserhaltung verwendet. Der Impuls beschreibt den mechanischen Bewegungszustand eines physikalischen Objekts. Der Impuls ist eine Erhaltungsgrösse, das heisst in einem physikalischen System bleibt die Summe aller Impulse konstant (Mgeladze 2024). Je schneller ein Körper sich bewegt und je grösser seine Masse ist, desto grösser ist auch der Impuls.

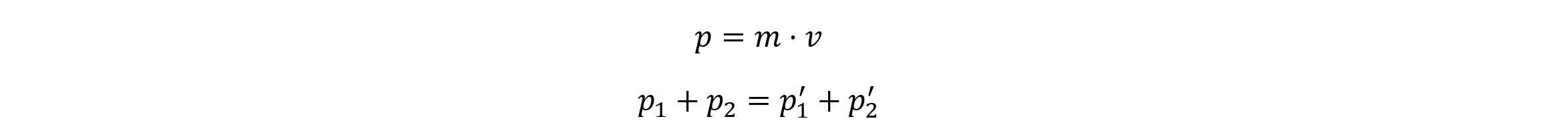
Der Gesamtimpuls vor einer Wechselwirkung ist gleich dem Gesamtimpuls nachher. Bei der Szene ist der Gesamtimpuls vor einem Abschuss 0. Die Formel wird also nach der Geschwindigkeit des Panzers aufgelöst.

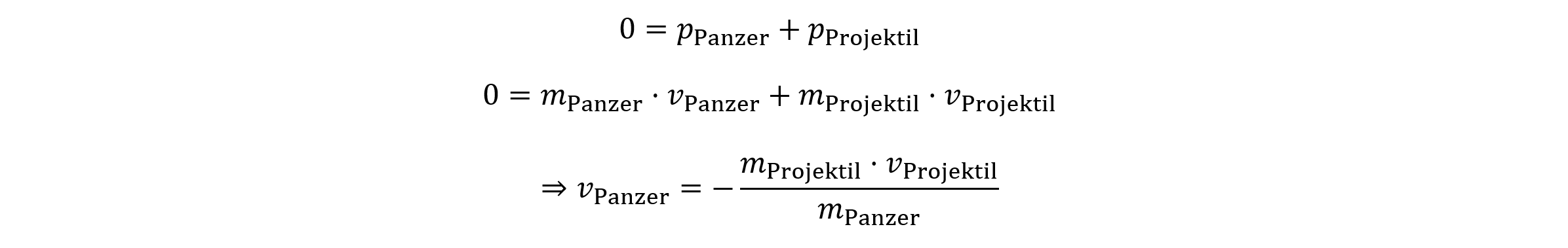
Nun kann der Betrag der Rückstossgeschwindigkeit ausgerechnet werden mit einer Panzermasse von 17’463.31 Kilogramm, einer Projektilmasse von 13.1 Kilogramm und einer Projektilgeschwindigkeit von 1021.08 m/s^2:

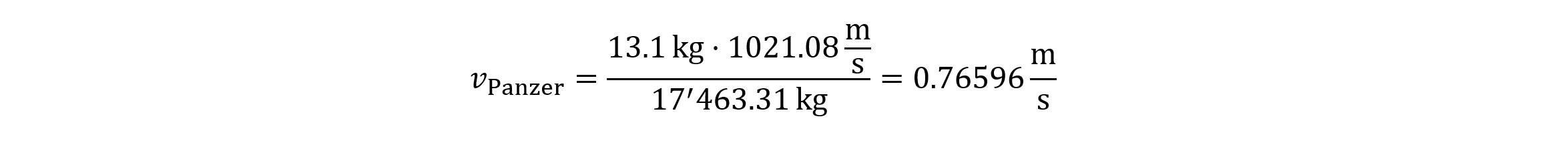
Die Rückstossgeschwindigkeit, die der Panzer erfährt beträgt 0.76596 m/s.

Zurückgelegte Distanz des Panzers

Die Kanone des Panzers schiesst nicht in einem 90° Winkel zum Boden, das bedeutet 0.76596 m/s ist nicht die effektive Geschwindigkeit des Panzers. In der Szene wird gesagt, dass die Kanone um 82° gedreht wird. Zum gleichen Zeitpunkt ist im Film zu sehen, dass die Panzerkanone aus der Normaleinstellung zur Seite gedreht wird. Dieser Faktor muss miteinbezogen werden.

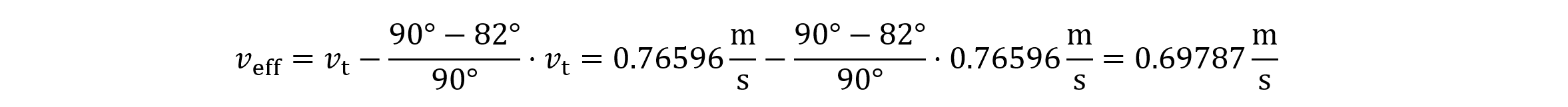
Die Kanone wird nach wenigen Schüssen erneut um 16° gedreht, jedoch ist unklar, nach wie vielen Schüssen genau. Auch später wird die Kanone erneut gedreht, es ist allerdings in der Szene nicht nachvollziehbar in welche Richtung. Deswegen wird für alle Schüsse mit einem Winkel von 82° gerechnet.
Alle fünf Sekunden wird die Geschwindigkeit erhöht, da ein neuer Schuss abgegeben wird. Der Luftwiderstand wird zunächst vernachlässigt.
Hier wird erneut mithilfe einer Exceltabelle die Geschwindigkeit von 0.69787 m/s alle fünf Sekunden zu der effektiven Geschwindigkeit addiert. Mit dieser Geschwindigkeit wird ausgerechnet, welche Distanz der Panzer in diesem Zeitintervall von fünf Sekunden zurücklegt.

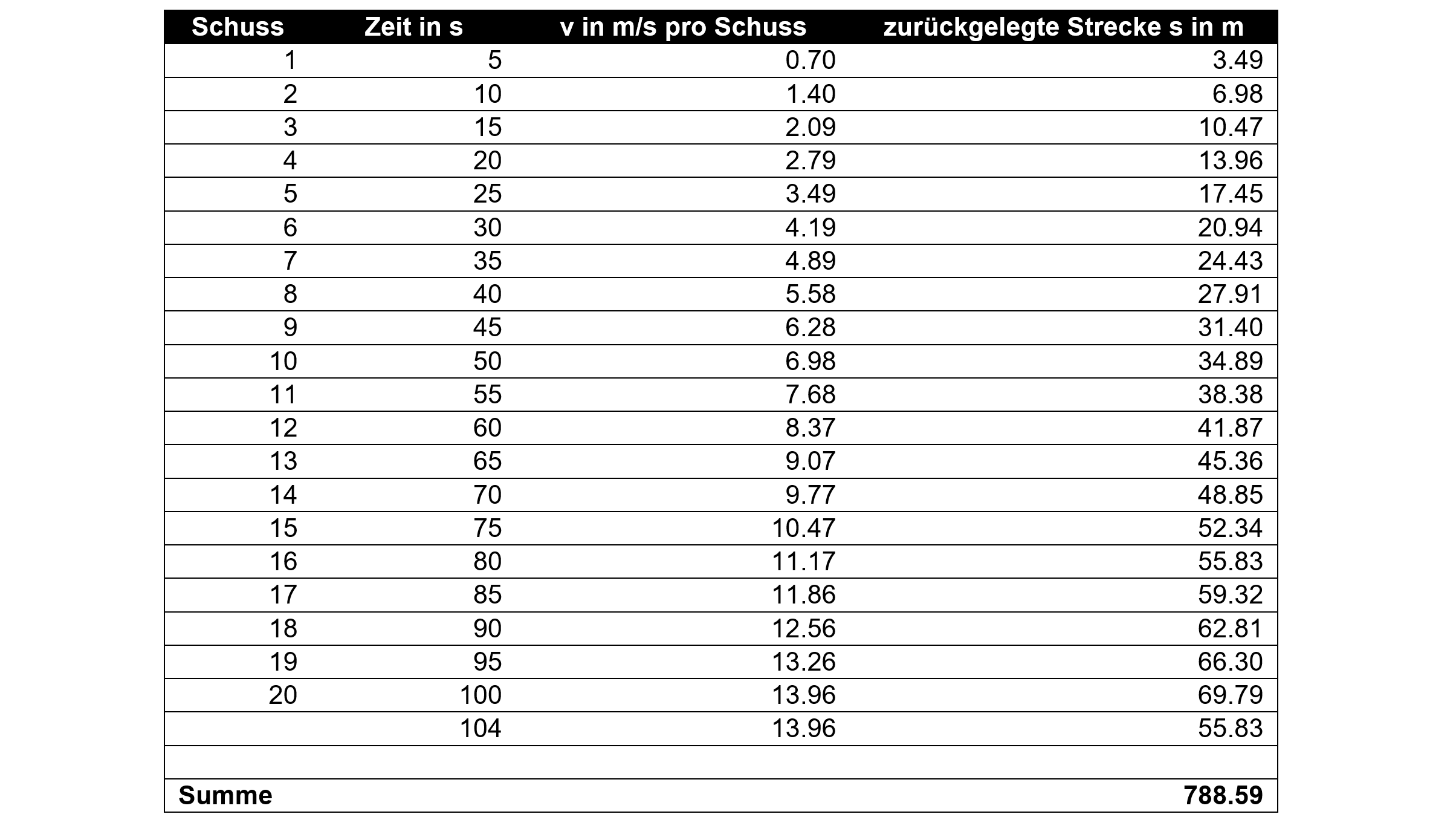
Der Panzer würde also in 104 Sekunden eine berechnete theoretische Strecke von 788.59 Meter zurücklegen. Dies reicht nicht um den See zu erreichen, welcher 804 Meter entfernt liegt. Die Szene «You can’t fly a tank» ist nicht realistisch.

Vergleich Film und Realität

Im Film ist zu sehen, wie sich der Panzer in grosser Höhe bereits über dem See befindet. Dies kann in Wirklichkeit nicht sein. Das Team würde es nicht schaffen, den Panzer so weit in horizontaler Richtung zu bewegen, geschweige denn mit so wenigen Schüssen wie im Film dargestellt. Der Rückstoss der Projektile ist dabei zu gering um den Panzer genügend weit zu bewegen. Zudem hätten sie im Anschluss keine Zeit, den Panzer zu verlangsamen oder die Oberflächenspannung des Sees mit einem Schuss zu durchbrechen, da sich der Panzer mit dem Team im inneren bereits kurz über dem Boden befände. Der Film stellt es so dar, als ob die Falldauer des Panzers sehr viel länger ist, als es in Wirklichkeit möglich ist.

Schafft es das A-Team den Panzer zu fliegen?

Im Film schafft es das Team, den Panzer 804 Meter mithilfe des Rückstosses in horizontaler Richtung zu bewegen. Die Szene ist aber nicht realistisch!
Wie berechnet, hat der Rückstoss der Kanone des Panzers zu wenig Kraft, um ihn in so kurzer Zeit und mit so wenigen Schüssen zu bewegen. Der Panzer würde nicht auf dem See aufschlagen, was natürlich für das A-Team verheerend wäre.